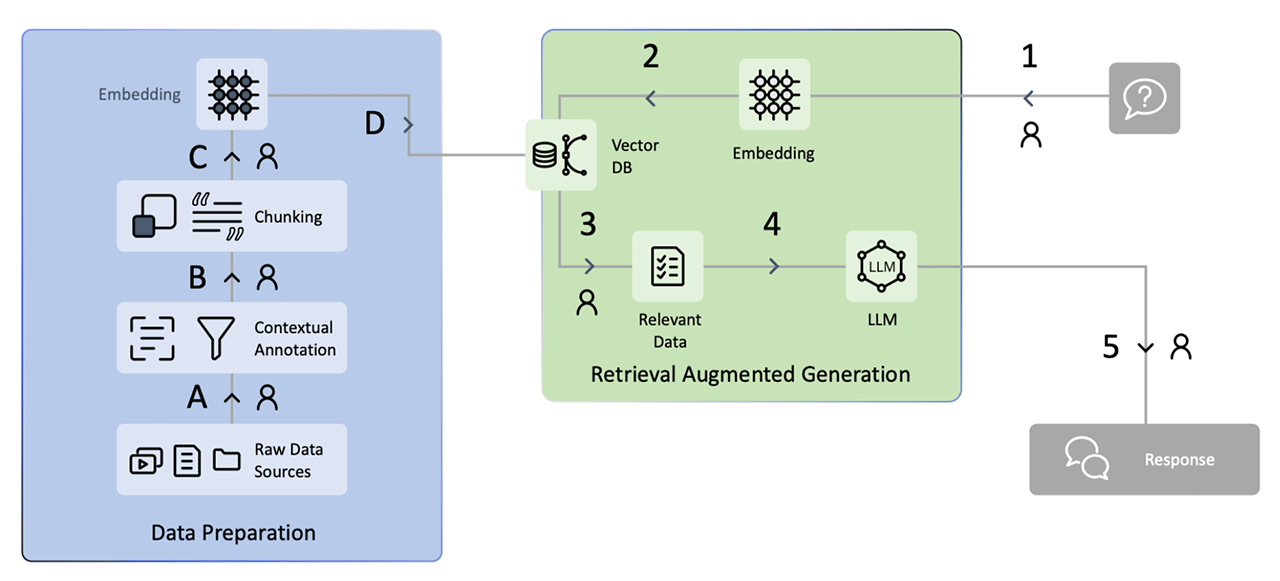
本节博客主要是通过“在排序数组中查找元素的第一个和最后一个位置”总结关于二分算法的左右界代码模板,有需要借鉴即可。
目录
- 1.题目
- 2.二分边界算法
- 2.1查找区间左端点
- 2.1.1循环条件
- 2.1.2求中点的操作
- 2.1.3总结
- 2.2查找区间右端点
- 2.1.1循环条件
- 2.1.2求中点的操作
- 2.1.3总结
- 2.3总结
- 3.参考解题代码
- 4.模板总结
- 5.总结
1.题目
题目链接:LINK

这个题要求我们求这个排序数组的一个元素的开始位置与结束位置。
可以用暴力求解的方法,把第一次出现的数字下标记录一下,最后一次记录一下,返回结果,除了复杂度差之外没什么不好的。
当然我们这里说一下二分算法的思想。之所以可以使用二分算法,这是因为该数组是有序的,可以利用二分算法的“二段性”将其分割。
用两次二分算法:
-
一方面,我们可以将整个数组分为大于等于t和小于t来找left点
-
另一方面,我们可以将整个数组分为大于t和小于等于t来找right点
但是这里有一些代码细节值得注意!!!
2.二分边界算法
2.1查找区间左端点

思考:我们在寻找左端点时候为什么要对数组按照小于t和大于等于t进行划分?
答:关键是因为我们要找左端点,左端点一定不可能在小于t的区间里。
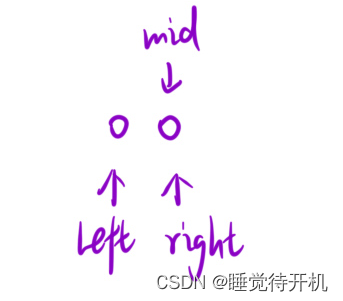
通过上面的图片可知,我们要想找到一个数的左端点,那么这个左端点(我们要寻找的点)一定不再大于t这个区域,所以我们可知
- mid < ret时,left = mid + 1
- mid >= ret时,right = mid
2.1.1循环条件
while(left < right)//... √
while(left <= right)//... ×
循环条件选:left < right
这里为什么不是left <= right 呢?
- left==right的情况下,即是最后结果,无需进行重复判断。
- 可能有些情况下会出现死循环问题
下面是对上面两个理由进行论证:
在所有可能情况中,无非存在三种情况, - ①left与right中间存在要找的ret点

此时,mid = ret,mid == right,那么left = mid,会不断进入循环,陷入死循环。 - ②left与right中间所有点全部大于我们要找的右端点

到了最后,mid > ret, mid = right,right = mid,会存在死循环问题 - ③left与right中间所有点全部小于我们要找的右端点

mid < ret,left = mid + 1,不会出现死循环问题。
2.1.2求中点的操作
我们求中点无非两种求法
①mid = left + (right - left) / 2; √
②mid = left + (right - left + 1) / 2; ×
这俩主要区别就是在数字个数是偶数情况下,①式取靠左的中点;②式取靠右的中点。
然后对于查找区间右端点而言,必须选用①式。
为什么,下面来进行解释?
如果选用②式,会存在下面情况:比如,mid指向right,然后mid所在的值>=ret值,就会不断死循环
注:if mid >= ret,right = mid;
2.1.3总结
在求目标值左端点时候,第一循环条件不能有等于,第二是求中点要用靠右中点。
2.2查找区间右端点
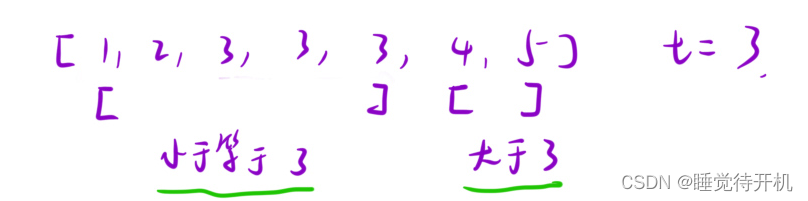
通过上面的图片可知,我们要想找到一个数的左端点,那么这个右端点(我们要寻找的点)一定不再大于t这个区域,所以我们可知
- mid <= ret时,left = mid
- mid > ret时,right = mid - 1
2.1.1循环条件
while(left < right)//... ×
while(left <= right)//... √
循环条件选:left < right
这里为什么不是left <= right 呢?
- left==right的情况下,即是最后结果,无需进行重复判断。
- 可能有些情况下会出现死循环问题
下面是对上面两个理由进行论证:
在所有可能情况中,无非存在三种情况,
- ①left与right中间存在要找的ret点

此时,mid = ret,mid == right,那么right = mid,会不断进入循环,陷入死循环。 - ②left与right中间所有点全部大于我们要找的右端点

到了最后,mid > ret,mid == right,right = mid - 1,不会出现死循环问题 - ③left与right中间所有点全部小于我们要找的右端点

mid < ret,left = mid,此时会出现死循环问题。
2.1.2求中点的操作
我们求中点无非两种求法
①mid = left + (right - left) / 2; ×
②mid = left + (right - left + 1) / 2; √
这俩主要区别就是在数字个数是偶数情况下,①式取靠左的中点;②式取靠右的中点。
然后对于查找区间右端点而言,必须选用②式。
为什么,下面来进行解释?
如果选用①式,会存在下面情况:比如,mid指向left,然后mid所在的值<=ret值,left = mid,如此就会不断死循环
注:if mid <= ret,left = mid;
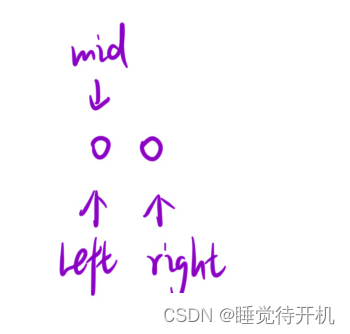
2.1.3总结
在求目标值右端点时候,第一循环条件不能有等于,第二是求中点要用靠右中点。
2.3总结
找左端点:
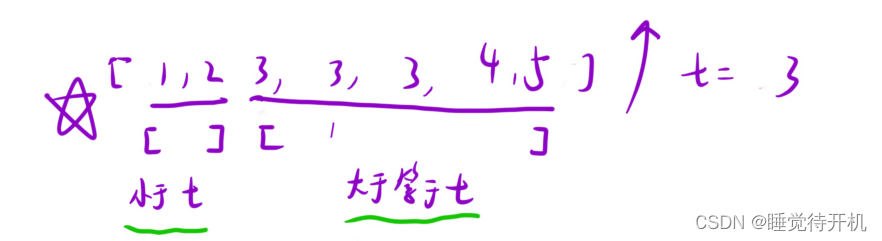
- mid < ret时,left = mid + 1
- mid >= ret时,right = mid
while(left < right)//...
mid = left + (right - left) / 2;
找右端点:
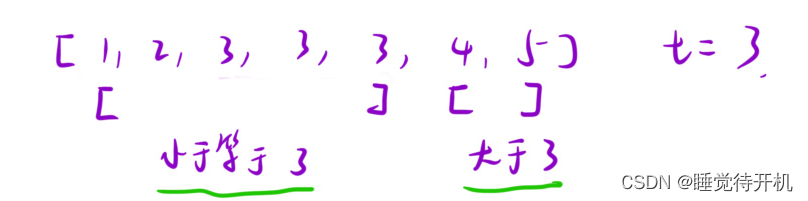
- mid <= ret时,left = mid
- mid > ret时,right = mid - 1
while(left < right)//...
mid = left + (right - left + 1) / 2;
根据上面的算法总结我们可以解决上面题目
3.参考解题代码
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
vector<int> ret;
//处理特殊情况
if(nums.size() == 0)
{
ret.push_back(-1);
ret.push_back(-1);
return ret;
}
int left = 0, right = nums.size() - 1;
//处理左端点
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] >= target)
{
right = mid;
}
else
{
left = mid + 1;
}
}
if(nums[left] == nums[right] && nums[left] == target)
{
ret.push_back(left);
}
else
{
ret.push_back(-1);
}
//处理右端点
left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else
{
left = mid;
}
}
if(nums[left] == nums[right] && nums[right] == target)
{
ret.push_back(right);
}
else
{
ret.push_back(-1);
}
return ret;
}
};
4.模板总结

5.总结
这个题目我感觉掌握了二分边界代码原理其实不难,重点肯定是那个二分边界算法原理,需要自己多理解一下。
EOF